Простые числа

Папирус Райнда, II век до нашей эры. Содержит таблицу, выражающую дроби вида 2/n через сумму дробей с числителями, равными единице, и различными знаменателями. Разложения дробей, знаменатели которых имеют общий делитель, похожи, что свидетельствует о том, что египтяне по крайней мере знали разницу между простым числом и составным.

Функция распределения простых чисел, или пи-функция (с числом π никак не связана), равняется числу простых чисел, меньших либо равных действительному числу x

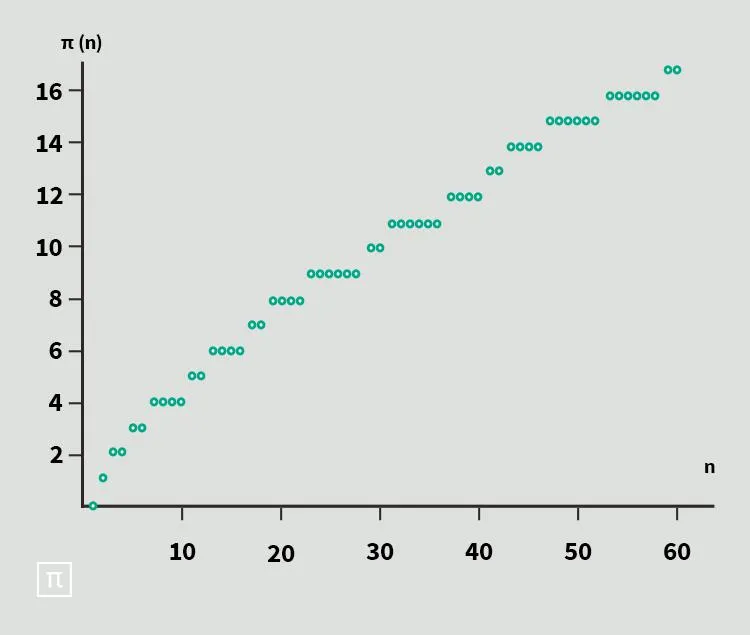
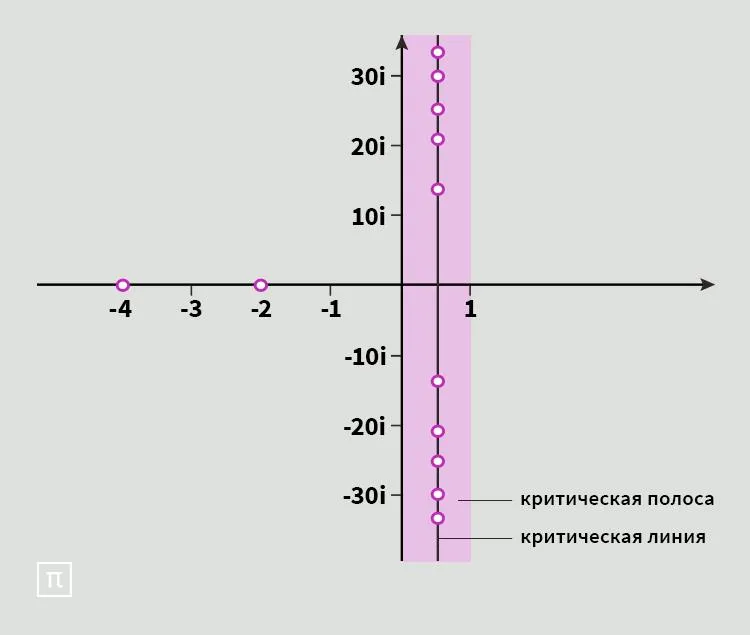
Все простые числа относятся к натуральным — тем, которые мы используем в обычной жизни для обозначения предметов. Однако множество натуральных чисел входит в другое множество — в действительные числа, которые представляют собой множество всех чисел на непрерывной числовой прямой. Кроме того, математики оперируют и другими множествами чисел, например комплексными. Как вам кажется, какое из этих утверждений не относится к числам вообще?

Про действительные числа можно думать как про некоторые операции, которые мы производим над точками прямой

Комплексные числа можно интерпретировать геометрически, их можно отождествить с точками плоскости

Гиперкомплексные числа Гамильтона — кватернионы — можно представить как трехмерные векторы, обладающие мерой вращения вокруг своей оси

Трехмерные гиперкомплексные числа представимы в виде трехмерных векторов в трехмерном пространстве